ぱわふる

検索条件

タグで絞り込みプログラミング(11) プログラミング::Perl(11) 勉強::心理学(1) 勉強::統計学(12) 小説(1)

日付で絞り込み 1月(1) 5月(7) 6月(4) 7月(1) 10月(1)

全14件 (1/3ページ) 記事本文を表示

2014/10/01(水)復学

６ヶ月の休学が終わってしまいました。

微妙な成果↓

IPA未踏：２次審査落ち
情報セキュリティスペシャリスト試験：４点差落ち
統計検定２級：合格

休学中に買って「読んだ」本は以下の通り。

「統計学入門 (基礎統計学)」
「日本統計学会公式認定　統計検定２級対応　統計学基礎」
「日本統計学会公式認定統計検定 2級公式問題集[2011～2013年]」
「統計学演習」
「マンガでわかる統計学回帰分析編」
「Webを支える技術 -HTTP、URI、HTML、そしてREST (WEB+DB PRESS plus)」
「タイポグラフィの基本ルール－プロに学ぶ、一生枯れない永久不滅テクニック－ (デザインラボ)」
「ロゴデザイン・ラブ! -僕の失敗と成功、みんなの話からわかるブランド・アイデンティティのつくり方」
「グラフィックデザイナーのためのユニバーサルデザイン実践テクニック51」
「書体の研究 for Digital Creators」
「SQLアンチパターン」
「達人に学ぶ SQL徹底指南書 (CodeZine BOOKS)」
「達人に学ぶDB設計徹底指南書」
「デザイニング・ウェブインターフェース ―リッチなウェブアプリケーションを実現する原則とパターン」
「インタフェースデザインの心理学 ―ウェブやアプリに新たな視点をもたらす100の指針」
「ハイパフォーマンスWebサイト ―高速サイトを実現する14のルール」
「Chef実践入門 ~コードによるインフラ構成の自動化 (WEB+DB PRESS plus)」
「Linuxサーバーセキュリティ徹底入門」
「ある日、爆弾がおちてきて (電撃文庫)」
「シナリオの基礎技術」
「ベストセラー小説の書き方 (朝日文庫) 」
「1週間でマスター小説を書くための基礎メソッド―小説のメソッド初級編」
「ハリウッド・リライティング・バイブル (夢を語る技術シリーズ)」
「小説講座売れる作家の全技術デビューだけで満足してはいけない」
「すごいライトノベルが書ける本　～これで万全！創作テクニック」
「新装版冲方丁のライトノベルの書き方講座 (このライトノベルがすごい!文庫)」
「ライトノベルの書き方キャラクターを立てるための設定・シーン・ストーリーの秘訣」
「文章読本 (中公文庫) 谷崎潤一郎」
「文字の組方ルールブック―タテ組編」
「本の知識―本に関心のあるすべての人へ!」
「新訳ふしぎの国のアリス (角川つばさ文庫)」
「日本語の作文技術 (朝日文庫) 」

「シナリオの基礎技術」「SQLアンチパターン」「文章読本 (中公文庫) 谷崎潤一郎」が特に役立った or 影響を受けた。

IPA未踏に出したアイディアは９５％はぐらいは既に実現してあるので、１０月１４日ぐらいには公開できるかなってとこです。

（土日も関係なく、ほぼ一日中コーディングで少し疲れました…）

コメント（0件）

2014/07/23(水)統計検定２級合格の軌跡

勉強::統計学

未踏２次審査の結果が出るまで時間があって、その間、ずっと統計学をやってました。

大学院生で落ちたら恥ずかしいレベルですが、勉強していなかったら落ちていたと思います。モチベーション保つには良い検定試験でした。

読んでルーズリーフにまとめた本は以下の通り。

マンガでわかる統計学

マンガでわかる統計学回帰分析編

統計学入門 (基礎統計学)

自分みたいにまともに統計学やったことがなければ、マンガでわかるシリーズで全体像を見て、赤本（統計学入門）をやるのがお勧めです。

あとは、以下の統計学会公式認定本をやれば合格できるかと思います。

公式認定の教科書は評判が悪いけど、どんな問題が出てどんな問題が出ないか確認するためにも必要でした。

日本統計学会公式認定　統計検定２級対応　統計学基礎

日本統計学会公式認定統計検定 2級公式問題集[2011～2013年]

自分は推定と検定の問題の解き方のパターンがいまいち分からなかったので、さらに以下の本をやりました。統計検定には出ない問題も一部含まれているけど、解法パターンがよくまとまっていて良書でした。

統計学演習

まともな統計学の講義を受けたことがある人は、東京大学出版会の赤本を教科書にして「統計学演習」で解き方を思い出して公式の過去問集やれば、手っ取り早く合格できるように感じました。

次は心理学検定でさらに統計学やる予定です。

コメント（0件）

2014/06/18(水)Perl Data Language 統計編 #11 「対数近似曲線を引く」

プログラミング::Perl勉強::統計学

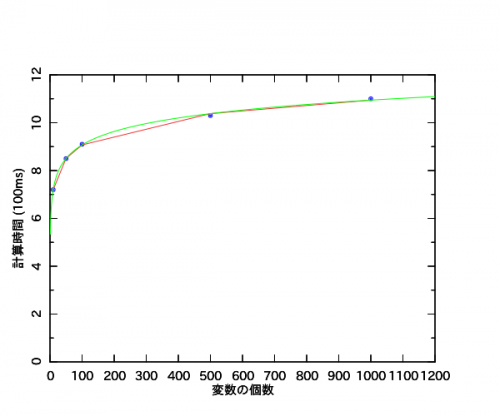
変数の個数xと計算時間yとの間に「y = b + a log_10 x」の関係があるときに、５個のデータで対数近似曲線を引く問題です。

「X = log_10 x」、「Y = y」とおいて「Y = b + aX」の形にすると解けます。

図は

青の点：データの散布
赤の折れ線：対数近似した折れ線
緑の曲線：対数近似した曲線

を表しています。

#!/usr/bin/env perl

use strict;
use warnings;
use feature qw/say/;
use PDL::Lite;
use PDL::Stats;
use PDL::Graphics::PLplot ();
use DDP filters => { -external => [ 'PDL' ] };

my $num_var = pdl [qw/10  50  100 500  1000/];
my $time    = pdl [qw/7.2 8.5 9.1 10.3 11.0/];

my $pl = PDL::Graphics::PLplot->new(
    DEV   => 'pngcairo',
    XLAB  => '変数の個数',
    XTICK => 100,
    NXSUB => 1,
    YLAB  => '計算時間 (100ms)',
    YTICK => 2,
    NYSUB => 2,
    BOX   => [ 0, 1200, 0, 12 ],
);

$pl->xyplot($num_var, $time, PLOTTYPE => 'POINTS', COLOR => 'BLUE', SYMBOLSIZE => 2);

my $num_var_log10 = log($num_var) / log(10);
my %result = $time->ols($num_var_log10, { PLOT => 0 });

$pl->xyplot($num_var, $result{y_pred}, PLOTTYPE => 'LINE', COLOR => 'RED');

my ($a, $b) = $result{b}->list;
my $x = pdl [ 0 .. 1200 ];
my $y = $b + $a * log($x) / log(10);

$pl->xyplot($x, $y, PLOTTYPE => 'LINE', COLOR => 'GREEN');

$pl->close;

コメント（0件）

2014/06/03(火)Perl Data Language 統計編 #10 「決定係数、残差プロット、自由度調整済み決定係数、標準誤差、P値」

プログラミング::Perl勉強::統計学

データは#09と同じく最高気温とアイスティーの注文数のデータです。

Perlで書くとこんな感じでした。

#!/usr/bin/env perl

use strict;
use warnings;
use feature qw/say/;
use PDL::Lite;
use PDL::Stats;
use PDL::Graphics::PLplot ();
use DDP filters => { -external => [ 'PDL' ] };

my $kion_max = pdl [qw/29 28 34 31 25 29 32 31 24 33 25 31 26 30/];
my $num_tea  = pdl [qw/77 62 93 84 59 64 80 75 58 91 51 73 65 84/];

my %result = $num_tea->ols($kion_max, { PLOT => 0 });

say "決定係数：";
say $result{R2}->sclr;
print "\n";

# 散布図と回帰直線の描画
my $pl = PDL::Graphics::PLplot->new(
    DEV  => 'pngcairo',
    FILE => 'manga.png',
    XLAB => '最高気温',
    YLAB => 'アイスティーの注文数',
    BOX  => [ 20, 35, 50, 100 ],
);

$pl->xyplot($kion_max, $num_tea, PLOTTYPE => 'POINTS', COLOR => 'BLUE', SYMBOLSIZE => 2);
$kion_max->qsort;
$pl->xyplot($kion_max, $result{y_pred}, PLOTTYPE => 'LINE', COLOR => 'RED');

$pl->close;

# 回帰残差の計算
my $residual = $num_tea - $result{y_pred};

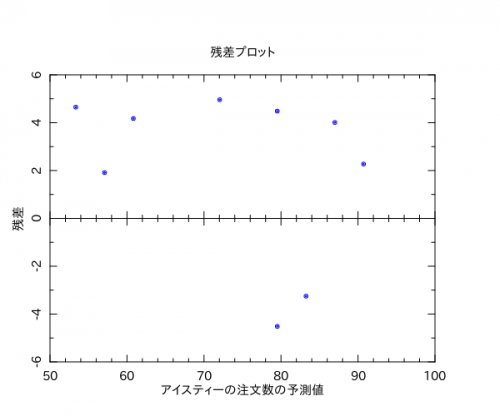
# 残差プロット
my $pl2 = PDL::Graphics::PLplot->new(
    DEV        => 'pngcairo',
    FILE       => 'manga_residual.png',
    TITLE      => '残差プロット',
    PLOTTYPE   => 'POINTS',
    COLOR      => 'BLUE',
    SYMBOLSIZE => 2,
    XLAB       => 'アイスティーの注文数の予測値',
    YLAB       => '残差',
    NYSUB      => 2,
    BOX        => [ 50, 100, -6, 6 ],
    XBOX       => 'abcnst',
);

$pl2->xyplot($result{y_pred}, $residual);
$pl2->close;

my $residual_squared = $residual ** 2;

say "残差平方和：";
say $residual_squared->sum;
say $result{ss_residual}->sclr;
print "\n";

say "残差の分散：";
my $residual_variance = $result{ss_residual}->sclr / ($kion_max->nelem - 2);
say $residual_variance;
print "\n";

say "自由度調整済み決定係数：";
say 1 - ($residual_variance / $num_tea->var_unbiased);
print "\n";

say "回帰係数の標準誤差：";
say $result{b_se};
print "\n";

say "P値：";
say sprintf("%.8f", $result{b_p}->sclr);

出力↓

決定係数：
0.822509288116695

残差平方和：
391.088105726872
391.088105726872

残差の分散：
32.5906754772394

自由度調整済み決定係数：
0.807718395459753

回帰係数の標準誤差：
[0.50124814  14.687267]

P値：
0.00000766

散布図と回帰直線は前回と同様です。

コメント（0件）

2014/06/03(火)Perl Data Language 統計編 #09 「回帰直線を引く」

プログラミング::Perl勉強::統計学

統計検定から少し寄り道して、「マンガでわかる統計学[回帰分析編]」の回帰直線を引くコードを書いていました。

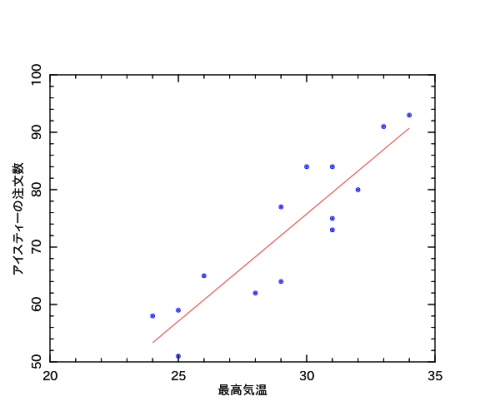
最高気温とアイスティーの注文数のデータに対する回帰直線です。

一方向性の因果関係を想定する場合、散布図は、X軸に原因系の変数をとってY軸に結果系の変数をとったものにするようです。

#!/usr/bin/env perl

use strict;
use warnings;
use feature qw/say/;
use PDL::Lite;
use PDL::Stats;
use PDL::Graphics::PLplot ();
use DDP filters => { -external => [ 'PDL' ] };

my $kion_max = pdl [qw/29 28 34 31 25 29 32 31 24 33 25 31 26 30/];
my $num_tea  = pdl [qw/77 62 93 84 59 64 80 75 58 91 51 73 65 84/];

say '相関係数：' . $kion_max->corr($num_tea);

my ($a, $b) = $num_tea->ols($kion_max, { PLOT => 0 })->list;

my $pl = PDL::Graphics::PLplot->new(
    DEV  => 'pngcairo',
    FILE => 'manga.png',
    XLAB => '最高気温',
    YLAB => 'アイスティーの注文数',
    BOX  => [ 20, 35, 50, 100 ],
);

$pl->xyplot($kion_max, $num_tea, PLOTTYPE => 'POINTS', COLOR => 'BLUE', SYMBOLSIZE => 2);
$kion_max->qsort;
$pl->xyplot($kion_max, $kion_max * $a + $b, PLOTTYPE => 'LINE', COLOR => 'RED');

$pl->close;

追記： olsメソッドの戻り値のy_predに予測値が入っているので、それを使うほうが効率いいですね。戻り値はPerlのコンテキストに応じて変わります。

#!/usr/bin/env perl

use strict;
use warnings;
use PDL::Lite;
use PDL::Stats;
use PDL::Graphics::PLplot ();

my $kion_max = pdl [qw/29 28 34 31 25 29 32 31 24 33 25 31 26 30/];
my $num_tea  = pdl [qw/77 62 93 84 59 64 80 75 58 91 51 73 65 84/];

my %result = $num_tea->ols($kion_max, { PLOT => 0 });

my $pl = PDL::Graphics::PLplot->new(
    DEV  => 'xcairo',
    XLAB => '最高気温',
    YLAB => 'アイスティーの注文数',
    BOX  => [ 20, 35, 50, 100 ],
);

$pl->xyplot($kion_max, $num_tea, PLOTTYPE => 'POINTS', COLOR => 'BLUE', SYMBOLSIZE => 2);
$kion_max->qsort;
$pl->xyplot($kion_max, $result{y_pred}, PLOTTYPE => 'LINE', COLOR => 'RED');

$pl->close;

出力される図は全く同一です。

コメント（0件）