ぱわふる

検索条件

タグで絞り込みプログラミング(11) プログラミング::Perl(11) 勉強::心理学(1) 勉強::統計学(12) 小説(1)

日付で絞り込み 1月(1) 5月(7) 6月(4) 7月(1) 10月(1)

全14件 (2/3ページ) 記事本文を表示

2014/06/02(月)Perl Data Language 統計編 #08 「系列相関とコレログラム」

プログラミング::Perl勉強::統計学

データは↓の「第２章/本文/Salary.data」

http://www.tokyo-tosho.co.jp/download/DL02122.zip

系列相関の式を見るだけでは分かりづらいので、PDLで計算＆グラフ描画です。

実行にも時間がかかるようになってきましたが、計算結果をハッシュとかでメモするなどの高速化の余地はあります。

#!/usr/bin/env perl

use strict;
use warnings;
use feature qw/say/;
use PDL::Lite;
use PDL::IO::Misc ();
use PDL::Graphics::PLplot ();
use DDP filters => { -external => [ 'PDL' ] };

my $infile       = 'Salary.data';
my $colnum_time  = 0;
my $colnum_tokyo = 2;

my ($yyyymm, $salary) = PDL->rcols($infile, { COLSEP => "t", INCLUDE => qr/[0-9]/ }, $colnum_time, $colnum_tokyo);

my $T = $yyyymm->nelem;
my $X = pdl [ 0 .. $T - 2 ]; # 月差
my $Y = PDL->null;           # 系列相関

for my $h (0 .. $T - 2)
{
    my $hensa_sekiwa = 0;
    my $s_h          = 0;
    my $s_plus_h     = 0;

    for my $i ( 0 .. ($T - 1) - $h )
    {
        my $y_bar_h      = 0;
        my $y_bar_plus_h = 0;

        for my $j ( 0 .. ($T - 1) - $h )
        {
            $y_bar_h      += $salary->at($j)    / ($T - $h);
            $y_bar_plus_h += $salary->at($j+$h) / ($T - $h);
        }

        $s_h      += ($salary->at($i) - $y_bar_h) ** 2;
        $s_plus_h += ($salary->at($i+$h) - $y_bar_plus_h) ** 2;

        $hensa_sekiwa += ($salary->at($i) - $y_bar_h) * ($salary->at($i+$h) - $y_bar_plus_h);
    }

    $s_h      = sqrt $s_h;
    $s_plus_h = sqrt $s_plus_h;

    my $r_h = $hensa_sekiwa / ($s_h * $s_plus_h);
    $Y = $Y->append($r_h);

    say $r_h;
}

my $pl = PDL::Graphics::PLplot->new(
    DEV      => 'pngcairo',
    FILE     => 'correlogram.png',
    PAGESIZE => [1800, 700],
    TITLE    => '東京の給与データのコレログラム',
    COLOR    => 'BLUE',
    XLAB     => '月差',
    XTICK    => 6,
    NXSUB    => 3,
    YLAB     => '系列相関',
);

$pl->xyplot($X, $Y);
$pl->close;

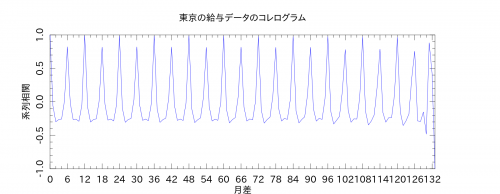
統計検定のテキストによると、縦軸を系列相関、横軸を時間差にしたものをコレログラムというらしい。テキスト通り、６ヶ月差と１２ヶ月差で周期性が見られました。

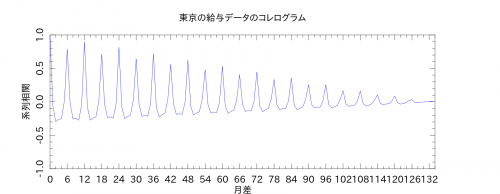
ちなみに、「PDL::Stats」のメソッドでやると↓のようになりました。系列相関係数の定義式が本によって違うんだけど、とりあえず統計検定２級のテキストに従っておけばいいのだろうか。

#!/usr/bin/env perl

use strict;
use warnings;
use feature qw/say/;
use PDL::Lite;
use PDL::Stats;
use PDL::IO::Misc ();
use PDL::Graphics::PLplot ();
use DDP filters => { -external => [ 'PDL' ] };

my $infile       = 'Salary.data';
my $colnum_time  = 0;
my $colnum_tokyo = 2;

my ($yyyymm, $salary) = PDL->rcols($infile, { COLSEP => "t", INCLUDE => qr/[0-9]/ }, $colnum_time, $colnum_tokyo);

my $X = pdl [ 0 .. $yyyymm->nelem - 1 ]; # 月差
my $Y = $salary->acf;

my $pl = PDL::Graphics::PLplot->new(
    DEV      => 'pngcairo',
    FILE     => 'correlogram.png',
    PAGESIZE => [1800, 700],
    TITLE    => '東京の給与データのコレログラム',
    COLOR    => 'BLUE',
    XLAB     => '月差',
    XTICK    => 6,
    NXSUB    => 3,
    YLAB     => '系列相関',
    BOX      => [ $X->minmax,  -1.0, 1.0 ],
);

$pl->xyplot($X, $Y);
$pl->close;

コメント（0件）

2014/05/30(金)Perl Data Language 統計編 #07 「標準化（Z）得点、偏差値（T）得点、変動係数、（やらしい）散布図、相関係数」

プログラミング::Perl勉強::統計学

１０人の２回の試験結果の分析です。

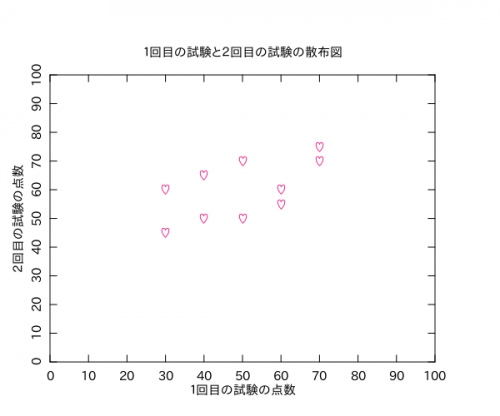
PLplotでどうやって散布図書くのかと思ったけど、PLOTTYPEをPOINTSに変えれば散布図になりました。使えるSYMBOLは「http://search.cpan.org/~dhunt/PDL-Graphics-PLplot-0.67/plplot.pd#SYMBOL」を参照。適当にハートマークのプロットの散布図にしてみました（謎）。

コードはループ中にavgメソッドがあったりとあまり効率よくなさそうですが、短く書くのを優先しました。（おそらく平均とかは別の変数に格納しておくほうが速いと思われる）

相関係数は「PDL::Stats」はN-1じゃないほうで計算しているけど、相関係数の定義式ではNでもN-1でも分母分子はNまたはN-1が割って１になるため、この違いは関係なくなります。

相関係数はおよそ0.6で、ぼちぼち相関ありって感じです。

#!/usr/bin/env perl

use strict;
use warnings;
use feature qw/say/;
use PDL::Lite;
use PDL::Stats;
use PDL::IO::Misc ();
use PDL::Graphics::PLplot ();
use DDP filters => { -external => [ 'PDL' ] };

# 試験結果
# Aさん .. Jさんの順番で並んでいる
my $first  = pdl [qw/30 30 40 40 50 50 60 60 70 70/];
my $second = pdl [qw/45 60 50 65 70 50 55 60 70 75/];

say "１回目の試験の平均　　：" . sprintf("%.1f", $first->avg);
say "１回目の試験の標準偏差：" . sprintf("%.1f", $first->stdv_unbiased);
say "２回目の試験の平均　　：" . sprintf("%.1f", $second->avg);
say "２回目の試験の標準偏差：" . sprintf("%.1f", $second->stdv_unbiased);
print "\n";

# 標準化
my $first_standardized  = ($first  - $first->avg)  / $first->stdv_unbiased;
my $second_standardized = ($second - $second->avg) / $second->stdv_unbiased;

say "Cさんの１回目と２回目の標準化（Z）得点：";
my $c_san_num = 2;
printf( "%.2f", $first_standardized->at($c_san_num) );
print " ";
printf( "%.2f", $second_standardized->at($c_san_num) );
print "\n";
print "\n";

say "みんなの偏差値（T得点）：";
my $first_t  = $first_standardized  * 10 + 50;
my $second_t = $second_standardized * 10 + 50;
say "１回目：";
printf("%.1f ", $_) for $first_t->list;
print "n";
say "２回目：";
printf("%.1f ", $_) for $second_t->list;
print "\n";
print "\n";

say "１回目の変動係数：" . $first->stdv_unbiased  / $first->avg;
say "２回目の変動係数：" . $second->stdv_unbiased / $second->avg;
print "\n";

say "１回目の試験と２回目の試験の相関係数：";
say sprintf( "%.3f", $first->corr($second) );

# 一応、専用メソッドを使わずに相関係数を求めてみる
my $sxy = 0;

for my $i ($first->listindices)
{
    $sxy += ($first->at($i) - $first->avg) * ($second->at($i) - $second->avg);
}

$sxy /= $first->nelem - 1;

say sprintf( "%.3f", $sxy / ($first->stdv_unbiased * $second->stdv_unbiased) );

my $pl = PDL::Graphics::PLplot->new(
    DEV        => 'xcairo',
    TITLE      => '１回目の試験と２回目の試験の散布図',
    XLAB       => '１回目の試験の点数',
    XTICK      => 10,
    NXSUB      => 1,
    YLAB       => '２回目の試験の点数',
    YTICK      => 10,
    NYSUB      => 1,
    COLOR      => 'DEEPPINK',
    PLOTTYPE   => 'POINTS',
    SYMBOL     => 742, # ハートマーク
    SYMBOLSIZE => 1.5,
);

$pl->xyplot($first, $second, BOX => [ 0, 100, 0, 100 ]);
$pl->close;

１回目の試験の平均　　：50.0
１回目の試験の標準偏差：14.9
２回目の試験の平均　　：60.0
２回目の試験の標準偏差：10.0

Cさんの１回目と２回目の標準化（Z）得点：
-0.67 -1.00

みんなの偏差値（T得点）：
１回目：
36.6 36.6 43.3 43.3 50.0 50.0 56.7 56.7 63.4 63.4 
２回目：
35.0 50.0 40.0 55.0 60.0 40.0 45.0 50.0 60.0 65.0 

１回目の変動係数：0.298142396999972
２回目の変動係数：0.166666666666667

１回目の試験と２回目の試験の相関係数：
0.596
0.596

コメント（0件）

2014/05/30(金)Perl Data Language 統計編 #06 「時系列データの折れ線グラフ」

プログラミング::Perl勉強::統計学

データ↓
http://www.tokyo-tosho.co.jp/download/DL02122.zip

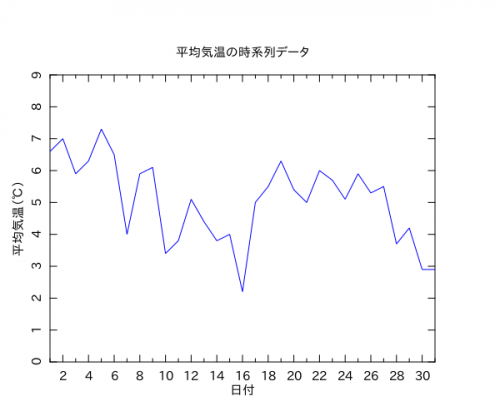
問1.1の7)は平均気温の変化を時系列データとして折れ線グラフで描けという問題。これは瞬殺できる問題ですな。

#!/usr/bin/env perl

use strict;
use warnings;
use PDL::Lite;
use PDL::IO::Misc ();
use PDL::Graphics::PLplot;
use DDP filters => { -external => [ 'PDL' ] };

my $infile        = 'weather.csv';
my $colnum_hizuke = 0;
my $colnum_kion   = 1;

my ($hizuke, $heikin_kion) = PDL->rcols($infile, { COLSEP => ',', INCLUDE => qr/[0-9]/ }, $colnum_hizuke, $colnum_kion);

my $pl = PDL::Graphics::PLplot->new(
    DEV   => 'xcairo',
    TITLE => '平均気温の時系列データ',
    XLAB  => '日付',
    XTICK => 2,
    NXSUB => 2,
    YLAB  => '平均気温（℃）',
    YTICK => 1,
    NYSUB => 1,
    COLOR => 'BLUE',
);

$pl->xyplot($hizuke, $heikin_kion, BOX => [ $hizuke->minmax, 0, int($heikin_kion->max) + 2 ]);
$pl->close;

コメント（0件）

2014/05/30(金)Perl Data Language 統計編 #05 「四分位数と箱ひげ図」

プログラミング::Perl勉強::統計学

データ↓
http://www.tokyo-tosho.co.jp/download/DL02122.zip

問1.1の6)です。

四分位数は、統計検定の試験とかで手計算でやるときは

昇順ソート
中央値（Q2）を求める
中央値点より小さいほうの中央値（Q1）を求める
中央値点より大きいほうの中央値（Q3）を求める

が一番楽かな。統計検定では四分位数の計算方法は定まっていないようなので、一番楽な計算方法でやりましょう。

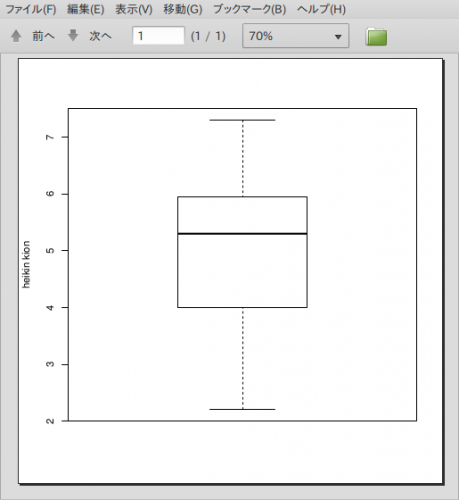
コードは以下の通りですが、箱ひげ図はPLplotだと大変なのでRで描画しました。

#!/usr/bin/env perl

use strict;
use warnings;
use feature qw/say/;
use Statistics::R;
use PDL::Lite;
use PDL::IO::Misc ();
use PDL::Graphics::PLplot;
use DDP filters => { -external => [ 'PDL' ] };

my $infile      = 'weather.csv';
my $infile_utf8 = 'weather_utf8.csv';

# 箱ひげ図はRで描画
my $R = Statistics::R->new;
$R->run(qq|weather <- read.csv('$infile_utf8')|);
$R->run(qq|boxplot(weather$平均気温, ylab='heikin kion', xlab='', range=0, data=weather)|);

# 四分位数はPerlで
my $colnum = 1;
my $heikin_kion = PDL->rcols($infile, { COLSEP => ',', INCLUDE => qr/[0-9]/ }, $colnum);

$heikin_kion .= $heikin_kion->qsort;

say '昇順での順位と値';

for my $i ($heikin_kion->listindices)
{
    say $i + 1 . ' ' . $heikin_kion->at($i);
}

print 'n';

say 'Q1: ' . PDL::Ufunc::pct($heikin_kion, 0.25);
say 'Q2: ' . PDL::Ufunc::pct($heikin_kion, 0.5);
say 'Q3: ' . PDL::Ufunc::pct($heikin_kion, 0.75);

出力：

コメント（0件）

2014/05/29(木)Perl Data Language 統計編 #04 「平均、分散、標準偏差」

プログラミング::Perl勉強::統計学

データ↓
http://www.tokyo-tosho.co.jp/download/DL02122.zip

問1.1の5)はPDL::Stats を使うと一撃。ですが、勉強にならないので一応普通に計算した場合も載せました。分散を計算するには平均を計算しないといけないので、そこで自由度が１減ると考えて不偏分散を使って計算しました。（統計検定２級のテキストを参照）

#!/usr/bin/env perl

use strict;
use warnings;
use feature qw/say/;
use PDL::Lite;
use PDL::Stats;
use PDL::IO::Misc ();
use DDP filters => { -external => [ 'PDL' ] };

my $infile = 'weather.csv';
my $colnum = 1;
my $heikin_kion = PDL->rcols($infile, { COLSEP => ',', INCLUDE => qr/[0-9]/ }, $colnum);

say "　　平均：" . sprintf("%.3f", $heikin_kion->avg);
say "　　分散：" . sprintf("%.3f", $heikin_kion->var_unbiased);
say "標準偏差：" . sprintf("%.3f", $heikin_kion->stdv_unbiased);
print "\n";


say "専用メソッドを使わずに分散と標準偏差を計算";

my $avg = $heikin_kion->avg;
my $sum = 0;

for my $i (0 .. $heikin_kion->nelem - 1)
{
    my $hensa = $heikin_kion->at($i) - $avg;
    $sum += $hensa ** 2;
}

my $variance = $sum / ($heikin_kion->nelem - 1);

say "　　分散：" . sprintf("%.3f", $variance);
say "標準偏差：" . sprintf("%.3f", sqrt $variance);

　　平均：5.055
　　分散：1.669
標準偏差：1.292

専用メソッドを使わずに分散と標準偏差を計算
　　分散：1.669
標準偏差：1.292

コメント（0件）