2014/05/30(金)Perl Data Language 統計編 #07 「標準化(Z)得点、偏差値(T)得点、変動係数、(やらしい)散布図、相関係数」
10人の2回の試験結果の分析です。
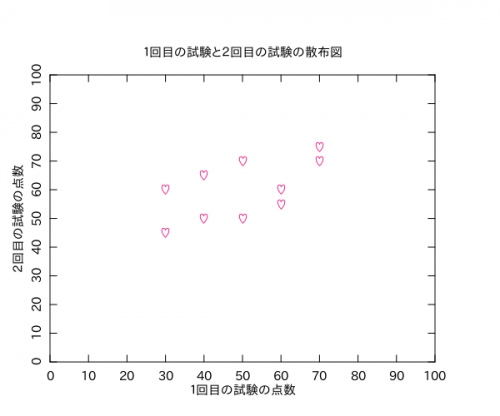
PLplotでどうやって散布図書くのかと思ったけど、PLOTTYPEをPOINTSに変えれば散布図になりました。使えるSYMBOLは「http://search.cpan.org/~dhunt/PDL-Graphics-PLplot-0.67/plplot.pd#SYMBOL」を参照。適当にハートマークのプロットの散布図にしてみました(謎)。
コードはループ中にavgメソッドがあったりとあまり効率よくなさそうですが、短く書くのを優先しました。(おそらく平均とかは別の変数に格納しておくほうが速いと思われる)
相関係数は「PDL::Stats」はN-1じゃないほうで計算しているけど、相関係数の定義式ではNでもN-1でも分母分子はNまたはN-1が割って1になるため、この違いは関係なくなります。
相関係数はおよそ0.6で、ぼちぼち相関ありって感じです。
#!/usr/bin/env perl
use strict;
use warnings;
use feature qw/say/;
use PDL::Lite;
use PDL::Stats;
use PDL::IO::Misc ();
use PDL::Graphics::PLplot ();
use DDP filters => { -external => [ 'PDL' ] };
# 試験結果
# Aさん .. Jさんの順番で並んでいる
my $first = pdl [qw/30 30 40 40 50 50 60 60 70 70/];
my $second = pdl [qw/45 60 50 65 70 50 55 60 70 75/];
say "1回目の試験の平均 :" . sprintf("%.1f", $first->avg);
say "1回目の試験の標準偏差:" . sprintf("%.1f", $first->stdv_unbiased);
say "2回目の試験の平均 :" . sprintf("%.1f", $second->avg);
say "2回目の試験の標準偏差:" . sprintf("%.1f", $second->stdv_unbiased);
print "\n";
# 標準化
my $first_standardized = ($first - $first->avg) / $first->stdv_unbiased;
my $second_standardized = ($second - $second->avg) / $second->stdv_unbiased;
say "Cさんの1回目と2回目の標準化(Z)得点:";
my $c_san_num = 2;
printf( "%.2f", $first_standardized->at($c_san_num) );
print " ";
printf( "%.2f", $second_standardized->at($c_san_num) );
print "\n";
print "\n";
say "みんなの偏差値(T得点):";
my $first_t = $first_standardized * 10 + 50;
my $second_t = $second_standardized * 10 + 50;
say "1回目:";
printf("%.1f ", $_) for $first_t->list;
print "n";
say "2回目:";
printf("%.1f ", $_) for $second_t->list;
print "\n";
print "\n";
say "1回目の変動係数:" . $first->stdv_unbiased / $first->avg;
say "2回目の変動係数:" . $second->stdv_unbiased / $second->avg;
print "\n";
say "1回目の試験と2回目の試験の相関係数:";
say sprintf( "%.3f", $first->corr($second) );
# 一応、専用メソッドを使わずに相関係数を求めてみる
my $sxy = 0;
for my $i ($first->listindices)
{
$sxy += ($first->at($i) - $first->avg) * ($second->at($i) - $second->avg);
}
$sxy /= $first->nelem - 1;
say sprintf( "%.3f", $sxy / ($first->stdv_unbiased * $second->stdv_unbiased) );
my $pl = PDL::Graphics::PLplot->new(
DEV => 'xcairo',
TITLE => '1回目の試験と2回目の試験の散布図',
XLAB => '1回目の試験の点数',
XTICK => 10,
NXSUB => 1,
YLAB => '2回目の試験の点数',
YTICK => 10,
NYSUB => 1,
COLOR => 'DEEPPINK',
PLOTTYPE => 'POINTS',
SYMBOL => 742, # ハートマーク
SYMBOLSIZE => 1.5,
);
$pl->xyplot($first, $second, BOX => [ 0, 100, 0, 100 ]);
$pl->close;
1回目の試験の平均 :50.0
1回目の試験の標準偏差:14.9
2回目の試験の平均 :60.0
2回目の試験の標準偏差:10.0
Cさんの1回目と2回目の標準化(Z)得点:
-0.67 -1.00
みんなの偏差値(T得点):
1回目:
36.6 36.6 43.3 43.3 50.0 50.0 56.7 56.7 63.4 63.4
2回目:
35.0 50.0 40.0 55.0 60.0 40.0 45.0 50.0 60.0 65.0
1回目の変動係数:0.298142396999972
2回目の変動係数:0.166666666666667
1回目の試験と2回目の試験の相関係数:
0.596
0.596